OptCtrlPoints: Finding the Optimal Control Points for Biharmonic 3D Shape Deformation

We propose OptCtrlPoints, a data-driven framework designed to identify the optimal sparse set of control points for reproducing target shapes using biharmonic 3D shape deformation. Control-point-based 3D deformation methods are widely utilized for interactive shape editing, and their usability is enhanced when the control points are sparse yet strategically distributed across the shape. With this objective in mind, we introduce a data-driven approach that can determine the most suitable set of control points, assuming that we have a given set of possible shape variations. The challenges associated with this task primarily stem from the computationally demanding nature of the problem. Two main factors contribute to this complexity: solving a large linear system for the biharmonic weight computation and addressing the combinatorial problem of finding the optimal subset of mesh vertices. To overcome these challenges, we propose a reformulation of the biharmonic computation that reduces the matrix size, making it dependent on the number of control points rather than the number of vertices. Additionally, we present an efficient search algorithm that significantly reduces the time complexity while still delivering a nearly optimal solution. Experiments on SMPL, SMAL, and DeformingThings4D datasets demonstrate the efficacy of our method. Our control points achieve better template-to-target fit than FPS, random search, and neural-network-based prediction. We also highlight the significant reduction in computation time from days to approximately 3 minutes.

Biharmonic coordinates is defined as the closed-form formulation of this optimization, namely $V = WC$. Here, $W$ called biharmonic weights is derived from the solution of the optimization. When the control points and resulting biharmonic weights are fixed, we calculate biharmonic weight only once. However, when computing deformations with different sets of control points, it is not feasible to leverage the prefactorization since the complementary selector matrix $T$ varies. That means, we need to calculate the prefactorization multiple times. Here, $TAT^{\top}$ is too large matrix to calculate its prefactorization multiple times.

To address this challenge, we introduce a reformulation of biharmonic weight that yields the same biharmonic weight matrix $W(S;A)$ while solving a linear system on a much smaller scale.

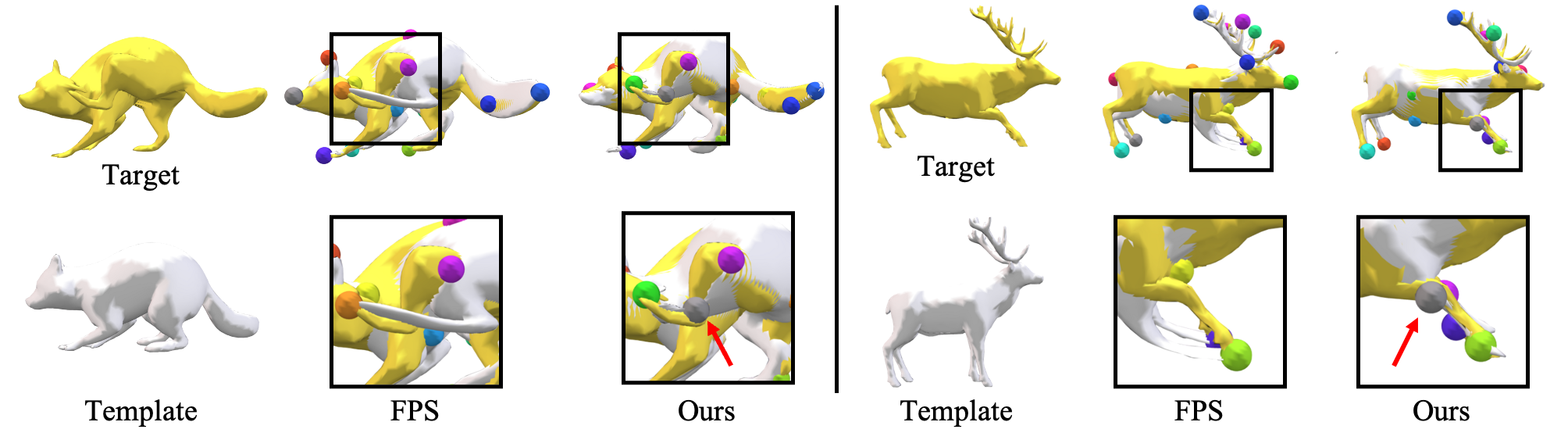
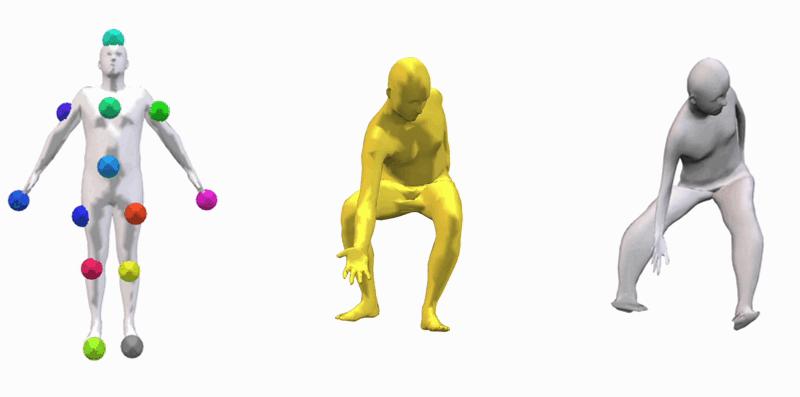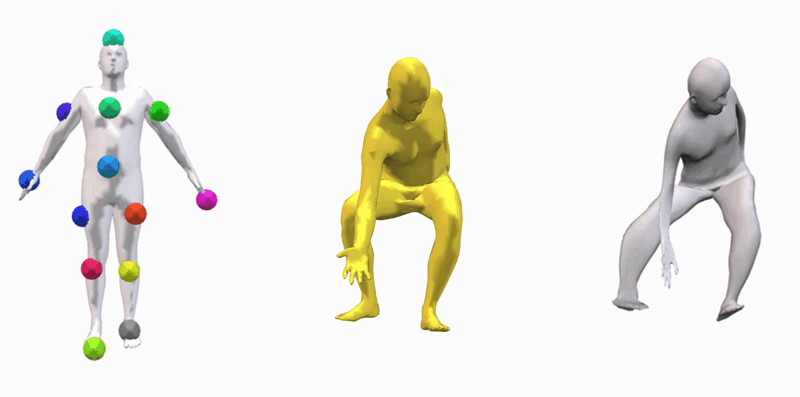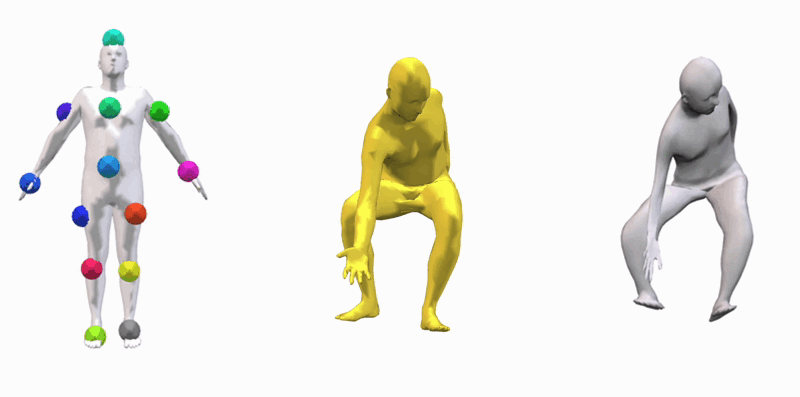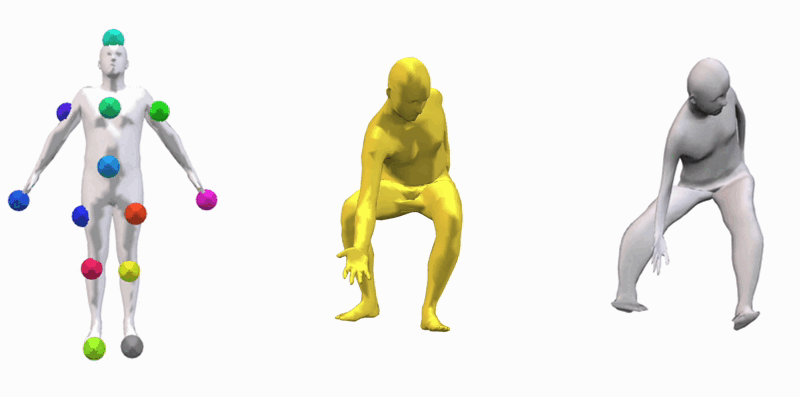OptCtrlPoints iteratively refines a set of control points starting from an initial configuration. First, establish $K$ partitions of the mesh by conducting a nearest neighbor mapping of all vertices to seed points, using the distance over the volume mesh graph as a measure of proximity.

In the first stage, we determine the partition to which the $k_{th}$ control point will move. We select the one of the sampled vertices that provides the minimum sum of distances between the template mesh and all the target shapes after deformation when substituting the current $k_{th}$ control point. By finding the vertex with the minimum sum of fitting distances, we identify the corresponding partitioned region for further exploration. After first stage, we have the best partition $l$ among $K$ partitions. The time complexity of this first stage is $O(K^2)$.

In the second stage, within the selected region $l$, we find the best vertex, similar to the first stage. We calculate the fitting error when substituting the current $k_{th}$ control point and select the one that minimizes the fitting error. The vertex selected during this step becomes the new $k_{th}$ control point for the subsequent iteration. Assuming an even partitioning of the template mesh with an equal number of vertices in each region, the average time complexity of this second stage is $O(N)$.

Therefore, the whole time complexity of OptCtrlPoints is $O(N+K^2)$. Our algorithm significantly reduces the computation time compared to the exhaustive search complexity of $O(N^K)$.